Fufho

LONGITUD DE CURVAS

Al considerar una curva definida por una función $f \left ( x \right )$ y su respectiva derivada $f' \left ( x \right )$ que son continuas en un intervalo [a, b], la longitud S del arco delimitado por a y b es dada por la ecuación:

(1) $S = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx$

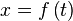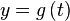En el caso de una curva definida paramétricamente mediante dos funciones dependientes de t como $x = f \left ( t \right )$ e $y = g \left ( t \right )$ , la longitud del arco desde el punto $(f(a), g(a)) \,$ hasta el punto $(f(b), g(b))\,$ se calcula mediante:

(2) $S = \int_{a}^{b} \sqrt{\left [ f' \left ( t \right ) \right ] ^2 + \left [ g' \left ( t \right ) \right ] ^2} \, dt$

Si la función esta definida por coordenadas polares donde la coordenadas radial y el ángulo polar están relacionados mediante $r = f (\theta)\,$ , la longitud del arco comprendido en el intervalo $[\alpha, \beta] \,$ , toma la forma:

(3) $S = \int_{\alpha}^{\beta} \sqrt{[ f (\theta)]^2 + \left [ f' (\theta) \right ] ^2} \, d \theta\$

En la mayoría de los casos, no hay una solución cerrada disponible y será necesario usar métodos de integración numérica. Por ejemplo, aplicar esta fórmula a la circunferencia de una elipse llevará a una integral elíptica de segundo orden.
Entre las curvas con soluciones cerradas están la catenaria, el círculo, la cicloide, la espiral logarítmica, la parábola, la parábola semicúbica y la línea recta.

Deducción de la fórmula para funciones de una variable

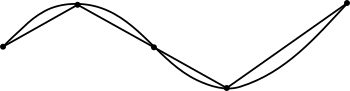
Supongamos que tenemos una curva rectificable cualquiera, regida por una función $f \left ( x \right )$ , y supongamos que queremos aproximar la longitud del arco de curva

S

que va desde un punto

a

a uno

b

. Con este propósito podemos diseñar una serie de triángulos rectángulos cuyas hipotenusas concatenadas "cubran" el arco de curva elegido tal como se ve en la figura. Para hacer a este método "más funcional" también podemos exigir que las bases de todos aquellos triángulos sean iguales a

Δ x

, de manera que para cada uno existirá un cateto

Δ y

asociado, dependiendo del tipo de curva y del arco elegido, siendo entonces cada hipotenusa igual a $\sqrt {\Delta x^2 + \Delta y^2}$ , al aplicarse el teorema pitagórico. Así, una aproximación de

S

estaría dada por la sumatoria de todas aquellas

n

hipotenusas desplegadas. Por eso tenemos que;

$S \sim \sum_{i=1}^n \sqrt { \Delta x_i^2 + \Delta y_i^2 }$

Pasemos a operar algebraicamente la forma en que calculamos cada hipotenusa para llegar a una nueva expresión;

$\sqrt { \Delta x^2 + \Delta y^2 }=\sqrt{ ({\Delta x^2 + \Delta y^2}).(\Delta x^2 / \Delta x^2)}=\sqrt { 1 + \Delta y^2 / \Delta x^2}.\Delta x=\sqrt { 1 + ({\Delta y / \Delta x})^2 }.\Delta x$

Luego, nuestro resultado previo toma la siguiente forma:

$S \sim \sum_{i=1}^n \sqrt { 1 + ({\Delta y_i / \Delta x_i})^2 }.\Delta x_i$

Ahora bien, mientras más pequeños sean estos

n

segmentos, mejor será la aproximación buscada; serán tan pequeños como deseemos haciendo que

Δ x

tienda a cero. Así,

Δ x

deviene en

d x

, y cada cociente incremental

Δ y i / Δ x i

se transforma en un

d y / d x

general, que es por definición $f ' \left ( x \right )$ . Dados estos cambios, nuestra aproximación anterior se convierte en una sumatoria más fina y ahora exacta, una integración de infinitos segmentos infinitesimales;
$S = \lim_{\Delta x_i \to 0} \sum_{i=1}^\infty \sqrt { 1 + ({\Delta y_i / \Delta x_i})^2 }.\Delta x_i = \int_{a}^{b} \sqrt { 1 + \left(\frac{dy}{dx}\right)^2 } dx = \int_{a}^{b} \sqrt{1 + \left [ f' \left ( x \right ) \right ] ^2} \, dx$

Fufho

lunes, 16 de mayo de 2011

Deducción de la fórmula para funciones de una variable

No hay comentarios:

Publicar un comentario